
K-2 Math: Even &
Odd
Today's Snack:
Line up a handful of red or green grapes in two lines. Count the number of
grapes in each line. Do you have the same number of grapes in each line? If so,
your total is "even." But if you have one more grape in one line than you do in
the other, your total is an "odd" number. Don't worry, they taste the same - so
eat them and enjoy a nice glass of white grape juice with them!
--------------------
Supplies:
15 pennies | scratch paper and
pencil
Learning the difference between
"even" and "odd" numbers is a good way to start learning about multiplication
and division, even when those math skills are still years ahead of you in
school.
A number is "even" if it can always be grouped by
two's. Count by two's: 2, 4, 6, 8, 10, 12 . . . and so on. Those are "even"
numbers.
If we say that a number is "odd," we
don't mean that it is weird. :>) We mean that the number CAN'T be evenly
grouped by two's. We will always have one left over if the number is "odd." So,
for example, 2 and 4 are "even," but 3 and 5 are "odd."
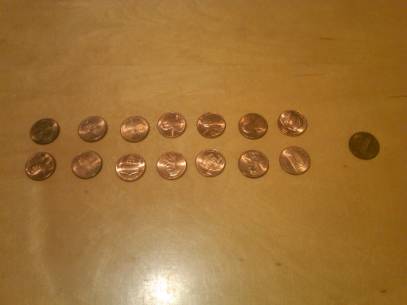
If you lay out 15 pennies in two rows, and have one left over,
does that tell you that 15 is an "even" number or an "odd" one?
Let's try it with some pennies. Lay out six pennies
on a table or desk. Put them in two rows. How many pennies do you have in each
row? (Three) Do you have any left over? (No) This shows that six is an "even"
number. When we divide it into two parts, we come out "even," with nothing left
over.
Now try this with seven pennies.
Place them in two rows. Now how many pennies do you have in each row? (Three in
one row, and four in the other) See how you don't end up with "even" rows? This
shows that seven is an "odd" number - when we divide it into two parts, we have
one left over.
Try this again with 10 pennies, 11,
and 15. Based on results, do you think 10, 11 and 15 are "even," or "odd"?
(10=even, 11=odd and 15=odd)
Now let's work a little bit with our
scratch paper on some basic addition problems, to see something else
interesting about "even" and "odd" numbers.
If you add two "even" numbers, do
you think the answer is probably "even," or "odd"? Let's try it - 2 is "even,"
so what if we add 2 + 2? The answer is 4 - another "even" number. In fact,
whenever you add two even numbers, the result will always be "even," too. Try
it with some other even numbers you know. Can you ever come up with an "odd"
answer when you add two "evens"? No.
But what if we add two "odd"
numbers? Will the answer be "odd," too? No! Let's try it - 3 is an "odd"
number, so let's add 3 + 3. The answer is 6 - which is an "even" number! Try
adding two other "odd" numbers, and see if the answer ever comes up "odd." How
about 5 + 7, or 9 + 11? Amazing! The answer is always "even." Here's the rule:
adding two "odd" numbers always produces an "even" answer.
The only time you ever get an "odd"
answer with addition is if you add an "even" number with an "odd" number. Let's
try it: 2 is even, and 3 is odd. Let's add them: 2 + 3. The answer, 5, is
"odd."
It's the same thing with
subtraction. Any time you subtract an "even" number from another "even" number,
the answer will be even. For example: 8 - 6 = 2 and 10 - 4 = 6. Any time you
subtract an "odd" number from another "odd" number, the answer will be "even,"
too. Examples: 9 - 7 = 2, 5 - 3 = 2.
The only time a subtraction answer
will be odd is if you subtract an "odd" number from an "even" one. For example:
10 - 7 = 3 and 8 - 7 = 1. Try a few examples of your own.
Numbers are odd, aren't they? But if
you master concepts like this, you won't just be "even" with your peers in
math. You'll be 'way ahead!